なぜどのように「わからなく」なるか 前編
2021.10.09
まなびやでは、たとえ受験科目に数学がない大学受験生であっても、時間が許せば最初に数学の授業をしている、という話を以前少し書きました。その中でもとくに重要なのがこれです。

問題自体は、中学生でもほとんどの生徒が解けます。
しかし大切なのは、生徒の頭の中で問題がどう扱われたかです。素朴に「aが2つとaが3つだから、合わせるとaは5つ」と考えても正しい答えが出ます。
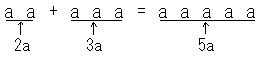
この理解は便利なようですが、実は大きな落とし穴があります。
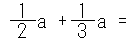
たとえばこの問題が解けません。分数くらいなら頭の中で解決できる力自慢がいるかもしれませんが、π(円周率)やe(ネイピア数)のような無理数だとか、単に文字でxとかyとか言われた場合には対応できなくなります。
より使い回しが広い理解は、たとえばこのようなものです。
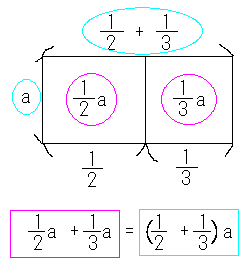
微積分が登場するまでの間は「掛け算は面積、面積は掛け算」だけで押し切れるので、いわゆる「同類項」は「高さが同じだから横に並べられる長方形」と同義だと見て大丈夫です。
これさえ覚えて帰ればいいだけなので、何の問題もないように見えます。しかし実際は、一筋縄ではありません。後編に続きます。

問題自体は、中学生でもほとんどの生徒が解けます。
しかし大切なのは、生徒の頭の中で問題がどう扱われたかです。素朴に「aが2つとaが3つだから、合わせるとaは5つ」と考えても正しい答えが出ます。
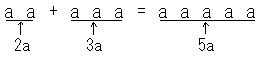
この理解は便利なようですが、実は大きな落とし穴があります。
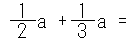
たとえばこの問題が解けません。分数くらいなら頭の中で解決できる力自慢がいるかもしれませんが、π(円周率)やe(ネイピア数)のような無理数だとか、単に文字でxとかyとか言われた場合には対応できなくなります。
より使い回しが広い理解は、たとえばこのようなものです。

微積分が登場するまでの間は「掛け算は面積、面積は掛け算」だけで押し切れるので、いわゆる「同類項」は「高さが同じだから横に並べられる長方形」と同義だと見て大丈夫です。
これさえ覚えて帰ればいいだけなので、何の問題もないように見えます。しかし実際は、一筋縄ではありません。後編に続きます。
 2021.10.09 19:59
|
2021.10.09 19:59
| 

