まなびやウェブログ

すでに更新を停止していますが、公開したい資料があったので掲載します。

重要英単語リスト
PDF

世界史や国際関係の勉強をしていて、まとまった情報が乏しく不便だなと感じている部分について、簡単にまとめたものをパブリックドメインのUTF-8テキストで公開します。

中国史の補足
ヨーロッパの言語と宗派
前13世紀までのメソポタミア
全部まとめて

-シリーズリンク-
ヨーロッパとイギリスの略年表

ファジィ論理（0か1かの2値論理でなく、0～1の実数からなる）
P and Q = min(P,Q)：最小
P or Q = max(P,Q)：最大
not P = 1 – P：補数
クリスプ集合（通常の意味での集合）が特徴関数（0か1を返す）で表現されるのに対し、ファジィ集合はメンバーシップ関数（0～1の実数を返す）で表現される。

ユニタリ行列は随伴行列を左乗しても右乗しても単位行列が得られる行列のこと。実数成分のみからなるユニタリ行列は直交行列と同義で、転置行列と逆行列が等しい正方行列になる。ユニタリ変換や直交変換は線形かつ等長な変換であり、計量ベクトル空間（内積を備えたベクトル空間）に作用させたとき内積を変えない。フーリエ変換は無限次直交変換の代表例で、任意の連続有界な関数を（無限の計算量を以ってすれば）正弦波の線形結合に変換できる。ウェーブレットを用いた音声変換や基底画像を用いた画像変換では、次数をかなり下げることができる。こう考えるとサンプリング（AD変換）も、時間や振幅などに近似精度を制限されながらの直交変換だと見なせそうなのだが、詳しい解説を見つけられなかった。結果的に得るのがデジタルデータ（ほぼベクトルと同義）なのだから、おそらくそうなのだろうと思う。

確率微分方程式はノイズ項（通常はガウス白色ノイズ）が入った微分方程式で、便宜上積分形で用いる。このとき当然、ホワイトノイズの積分（ウィーナー過程）を扱う必要があるのだが、それを系統立てたのが伊藤積分やストラトノビッチ積分。専門的な説明は一橋大学大学院商学研究科 高岡浩一郎先生の公演資料を参照。レッドノイズ（ブラウニアンノイズ）を得るだけなら、ホワイトノイズを離散化（サンプリング）して総和を取るとか、電気回路で積分器に熱雑音を流すとか、素人考えにもいくつか方法が思い浮かぶものの、おそらく「解析的に扱える」ことが重要なのだろう。上の資料だけでも私の理解をはるかに超えており、何の話をしているのかもピンとこないが、より数学寄りの話題については東京理科大学理工学部数学科 平場誠示先生の解説が詳しい。

余談ながら、平場先生はTeXエディタ雅理の作者としても活動されています。ウェブサイトに掲載された最初にという文書にある「大事なのは,色々な考え方ができるということで,数学とはそれを身に着けるための学問だと言っても良いかも知れない」という一節に、共感を覚えます。

-シリーズリンク-
前のメモ

自分が悩んだときのメモを備忘録として公開しておきます。同じ問題で悩んでいる人以外にはまったく無意味な情報なのであしからず。

スタイルシートの記述をcssファイルで

a:link, a:visited {普通の設定;}
p#hoge a:link, a:visited {部分的な設定;}

としていたところ、chromeがページ全体に「部分的な設定」を適用してしまうという現象に遭遇した。試行錯誤の結果

a:link, a:visited {普通の設定;}
p#hoge a {部分的な設定;}

のように、ID決め打ちの部分には擬似クラスを指定しないことで解決した。

なぜ擬似クラスのところがカスケードせず上書きになってしまうのか不思議ですが、とりあえず上記で動いている様子。

5年、50年、500年、5000年、5万年、50万年、500万年前のおもな出来事をまとめてみました。パブリックドメインで公開します。
500万年前から5年前までの年表
変化が加速すると「変えなくてはならないこと」と「変えてはいけないこと」の両方が、どんどん増えていきます。そのことを実感する助けになればと思います。

ピアソンのカイ2乗検定とフィッシャーの直接確率検定では、帰無仮説が異なる。カイ2乗検定の帰無仮説は平均効果が0であるというもので、プラスの効果とマイナスの効果が同確率で同程度に現れる場合は棄却されない。直接確率検定の帰無仮説は個体効果が0であるというもので、プラスの効果もマイナスの効果もない場合にのみ棄却されない。後者の方が強い条件であり「シャープな帰無仮説」と呼ばれる。カイ2乗検定にイェーツの連続性補正を施すと、直接確率検定の結果とよく近似するようになる。「フィッシャー検定」という呼称も一般的ではあるが、F検定と紛らわしい。カイ2乗検定は復元抽出の分布である二項分布に、直接確率検定は非復元抽出の分布である超幾何分布に基づく、らしいのだが二項分布からカイ2乗分布に乗り換える必然性がいまひとつピンとこない。

独立二群の平均値差に関するスチューデントのt検定とウェルチのt検定は、どちらも母集団が正規分布することを前提とするが、前者がさらに等分散を要求するのに対し、後者は非等分散であってもよいように補正してある。検定の多重性を避けるために、等分散であることが自明でないデータであればウェルチのt検定を用いるべき。F検定は正規分布に従う2つの群の標準偏差が等しいかどうか、正規分布に従い標準偏差が等しい2つの群の平均が等しいかどうか、のどちらか（だけ）に用いるのが無難。t検定の前に、KS検定などを行って前提の適合度を評価するのは差し支えない。

余談ながら、ディラックのデルタを正規分布関数の極限で近似する手法を調べていたときに、岡竜之介のブログという愉快なウェブログを発見したので紹介します。ディラックのデルタに対抗して「イプシロン」なる変な関数を勝手に、しかし真面目に作ってしまった話だとか、算数の問題を作るとき先生が密かにイラっとしている「通分して計算したら約分が必要なくなってしまう問題」をスッキリ解決するプログラムを作る話だとかが、どこか昔懐かしいテイストとともに掲載されています。数学IIIまで勉強した生徒なら、少し背伸びすれば面白おかしく読めると思います。

-シリーズリンク-
前のメモ＜＞次のメモ

イプシロンデルタ論法は一見面倒そうだが、ようするに、高校数学でいう「Δx」を無限に小さく「できることを保証」するための方法論である。

微分をライプニッツの記法で書いたときのdy/dxはもともと「Δy/ΔxについてΔx→0の極限を取ろう」という意図で、次元を意識しないときは「微分小」とか「無限小変分」などと呼ばれる。これを正確に理解するには外微分の知識が必要になり、本格的な数学にほんの少しだけ足を突っ込むことになってしまい、それはそれは恐ろしく大変なことになる。どうしても知りたい人は下記を参照。
http://www.math.titech.ac.jp/~kawahira/courses/kiso.html
http://sshmathgeom.private.coocan.jp/diffgeom/tangentvec.pdf
https://www.math.sci.hokudai.ac.jp/~ishikawa/kikaA08/08-kikaA-hosoku2.pdf
全微分（ないし一次微分形式）をこのように書く、という知識のところで立ち止まるのも方便ではないか。

高校範囲の知識でなんとなくのイメージが得られないか、と考えてみたところ、多変数関数を扱うときに意味が出てくる概念なのだから、変数を増やせばよさそう。ということで媒介変数関数の微分公式をイメージするのはどうだろうか。x=f(t)かつy=g(t)ならばdy/dx=g'(t)/g'(t)というアレである。ライプニッツの記法とラグランジュの記法を混ぜて書くのは奇妙だが、こうすると「dx=g'(t)なのかな」というイメージが、なんとなく沸いてくるような気がする。またyをxで2階微分するのをライプニッツの記法でd^2y/dx^2と書くが、これはd(dy/dx)/dxという風に繁分数で書いた方が誤解が少ないのではないか。こうしておけば、媒介変数表示でdy/dx=h(t)=g'(t)/g'(t)となっているときのd(dy/dx)/dx=[d(dy/dy)/dt]*[dt/dx]なんかも、より自然に理解できるように思う。

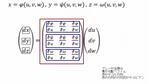
n個の変数X=(x1,x2...,xn)が像F=(f1,f2...,fm)をなし（どちらも列ベクトルとして考える）、すべてのfiがxjで偏微分可能なとき、i行j列が∂fi/∂xjとなる行列を、多変数ベクトル値関数Fのヤコビ行列という。全微分を与える表現行列だと見ることもできるし、Fの要素の勾配ベクトルを行として縦に積み上げたと見ることもできる。

-シリーズリンク-
前のメモ＜＞次のメモ

このところ少し数学の勉強をしていて、備忘録的にメモっておいたことや、なんとなく思いついたことなどを書き溜めるうちにけっこうな分量になったので、物の役には立たないでしょうが公開してみます。あくまで勉強中のメモで、どの程度正しい理解なのか私は知りません。

Aを行列、xとbを列ベクトルとして
A*x=bならば
A^-1*A*x=A^-1*b
x=A^-1*b
という演算ができる。線型方程式がn個の変数を持ちn本の一次方程式からなるとき、それらを行列表示したものをAとすると正方行列になるが、Aが正則である（逆行列をもつ）ならば、ベクトルxのi番目の成分xiは、Aのi列をbに置き換えた行列をAiとして、
xi=det(Ai)/det(A)
と一意に解くことができ、クラメールの規則とかクラメルの公式などと呼ばれる。

A^-1を求めるとき、実用上は掃き出し法などの方が計算量の増加が穏やかだが、余因子展開の方が原理がわかりやすい。Aのi行めとj列めを除いた行列をAijと書き、余因子Δijを
Δij=(−1)^(i+j)*det(Aij)
と定義する。この余因子を要素とするi行j列の行列をA^（流儀によってはC）、それを転置したものをA~（余因子行列）として、ライプニッツの明示公式から行列式の多重線型性を確認すれば、
A^-1=(1/det(A))*A~
が成り立つことがわかる。

n個の関数（実関数でも複素関数でもよい）f1,f2...,fnが区間I上でn−1階微分可能とするとき、f1の0～n-1階微分を縦に並べた列ベクトルf1(x),f2の0～n-1階微分を縦に並べた列ベクトルf2(x)...,fnの0～n-1階微分を縦に並べた列ベクトルfn(x)を横に並べて作った行列（i行j列成分が、fjのi-1階微分になる）の行列式をロンスキー行列式W(f1,f2...,fn)という。ロンスキー行列式（ロンスキアン）が「恒等的に0」でないとき、f1,f2...,fnからなる関数族は線形独立な解をもつ。厳密な証明はさておき、拡大係数行列で連立方程式を解く操作を確認すれば、おそらくそうなのだという納得はできよう。関数族が線形従属である条件は難しいようで、ペアノなどが考察を与えているらしい。

-シリーズリンク-
次のメモ

わざわざ断って配るほどのものではありませんが、パブリックドメインで公開します。

当初「イギリスの略年表」というタイトルで公開していましたが、まちゼミの資料用にヨーロッパ周辺の年表も作ったので、まとめてutf-8のテキストファイルにしました。
ヨーロッパ1、1万年前くらいまで
ヨーロッパ2、前8世紀くらいまで
ヨーロッパ3、4世紀末まで
ヨーロッパ4、8世紀始めまで
ヨーロッパ5、11世紀半ばまで
ヨーロッパ6、13世紀末まで
イギリス、18世紀まで
全部まとめて
一部参考資料のアドレスを文中に示してあります。

-シリーズリンク-
世界史関連の資料その2

表示される結果を確認しながらmathjaxを書くためのCGIスクリプトです。これもパブリックドメインで配布しますが、とても酷い書き方をしており安全性もゼロなので、中身を見て意味がわからない方は使用しないでください。

スクリプトファイル
動作サンプル

2020/12/3更新
バージョン13　デフォルト動作でgetメソッドを無効化
バージョン12　ヘッダとボディを分離、readme.txtを作成
バージョン11　あまりに酷いところを手直し
バージョン10　手元で使っていたものを公開

-参考外部リンク-
MathJaxの使い方@物理数学付録
MathJax で利用可能な TeX コマンド（非公式）@Green Company
LaTeX のような web ページの数式 :: MathJax@山本研究室

-2020/12/13追記-
後で調べてみたところ、TeXならオンラインサービスが豊富なよう。たとえば、
TeX を使ってみよう@奥村 晴彦
Some Things About TeX
LaTeX Base
など。