まなびやウェブログ

このところ国際情勢がせわしなくなっています。より広く多様な情報を得るために、海外のニュースを読むのも有効な手段でしょう。

ニュースサイトは品質が大きく変わってしまうことがありますが、この記事を書いている時点での私のお勧めは、Al Jazeera（アルジャジーラ）とteleSUR（テレスール）です。アルジャジーラは中東のカタール、テレスールは南米のベネズエラが本拠地で、国際ニュースはロイターやBBCから買っている記事も多いようですか、サイト自体が見やすく読みやすいのと、記事の取捨選択に独特のセンスがあるのが特徴です。

なお、無料で高性能な機械翻訳を提供しているサイトも複数あるので、英語が苦手な人は活用してみるとよいでしょう。海外報道機関の「日本語版サイト」から得られるのとは、かなり違った情報も見つかるはずです。

-参考外部リンク-
Al Jazeera（Jazeera Satellite Channel）
teleSUR
DeepL翻訳（無料版）
Google翻訳

中学校で理科を勉強したとき、空気は窒素8割くらいと酸素2割くらいが混ざったもので、窒素は少し軽く酸素は少し重い、と習いました。そのとき「だったら軽い窒素は空の上の方に集まって、地面近くの低いところは重い酸素ばっかりになるんじゃないか」と疑問に思ったのですが「でも風が吹いたりすれば混ざるか」と一人で納得した記憶があります。

この考え自体はそう大きな間違いではなかったのですが、実は、地球規模で見るとほんの少しだけ「分離」していることが確認されたという研究発表をウェブで見つけました。いやはや「多分こんな感じじゃないの」で済まさずにとことん追求することで、こんな微妙な違いにも気付いて確認することができるとは、目から鱗が落ちる思いです。

-参考外部リンク-
成層圏大気主成分の重力分離の発見とその大気循環研究への応用@
東北大学大学院理学研究科　大気海洋変動観測研究センター

とくに高校生相手の相談で、進路を決めるということは、何年かの間「住む場所」を決めることでもある、ということをよく話します。もちろん、習得したい技能だとか必要になる費用だとか、他にもっと重要な事柄があるのは間違いありませんが、住む場所によって得られる経験というのも見過ごせない要素でしょう。

私個人としては、田舎の人には都会の暮らしを、都会の人には田舎の暮らしを体験してみて欲しいという願いがありますが、もっと大切なことはそれを「選ぶ」意識だと思っています。ずっと同じ場所で暮らすのだとしても、世の中に「ここ」とは違う場所があるらしいことを知ったうえで、自分で材料を得て選んだ結果であれば、そうでない場合とはおのずと違いが生まれてくるだろうという確信があります。

情報の伝達はどんどん速く容易になっていますが、一方でいろいろな分極が進んでいます。都会と田舎、若者と老人、金持ちと貧乏人、男性と女性、日本人と外国人、他にもまだまだあるでしょう。格差とか分断といった否定的な言葉が使われることもありますが、世の中が多様になれば、小さいグループで固まりたい心情が強くなるのは自然なことです。そういう傾向が進めば進むほど、高くなってしまった「隔たり」を越えなければならない機会も増えます。自分自身も「選んだ結果」として今ここにいるのだ、という認識がもしあれば、大きな助けになるに違いありません。

リンクは記事の一番下にまとめておきましたが、ツイッター上で2年ちょっと前に開催された「丸いケーキを3等分する方法」を競うイベントの話題です。先に無難そうな回答例を紹介しておきましょう。小学生の知識でもできるやり方としては、内接正六角形を使うのが手っ取り早いでしょうか。

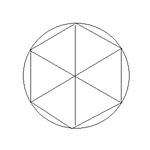
図はフリーハンドで描いているので不正確です。算数の範囲「だけ」で円の直径を引くには、ケーキの形をいったん紙に写して、半分折りにするくらいしかありませんが、天下り式の知識を使ってよいなら、定規を円周に当てて三角定規を接点に当てる、大きい三角定規の直角部分を円周に当てる、などの方法があります。中1で習う垂直二等分線の知識があれば、三角定規を使わず定木（長さを計れない直線を引けるだけの定規）とコンパスだけでOKです。直径さえわかれば、それを半分にすれば半径も中心もわかります。あとは、地道にやるなら正三角形を6つ作れば図のようになりますし、円周を半径と同じ長さの弦で6等分しても、結局同じことになります。直角の作り方は中1まで習いませんが、正三角形は小3で習うようです。

私が思いついたのは「4等分してから3等分」です。実は「直径を引いて、半径の垂直二等分線を引く」やり方の方が作業がスマートなのですが、それだと入賞作の「4等分線をイメージして切る」と結局同じになってしまいます。

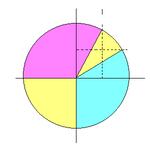
理屈としては、円を3等分する問題を扇形を3等分する問題に「落とし込んで」いるのがポイントで、こうやって切った方がきっと楽でしょう。この方法で数学的に正しい分割もできますが、ケーキを切る時にコンパスなんて使いたくないので、中心は目見当で適当に決め、直角も勘で切ります。もし自分の目の前に丸いケーキがあって、3等分しなければならなくなったら、きっとそうするだろうという確信があります。なお扇形を3等分するところは、算数の知識だけだと正三角形を作る（または分度器を使う）必要がありますが、sin(π/6) = cos(π/3) = 1/2がわかれば垂直二等分線で間に合います。中学校でルートを習うまで使えないsin(π/3) = cos(π/6) = {3^(1/2)}/2と違い、sin(π/6)は正三角形を半分にして長さを考えれば確認することができます。いわゆる「30-60の直角三角形」が、正三角形を2等分した図形であることは、覚えておくと少し得かもしれません。

数学クラスタが集まって本気で大喜利してみた(ISBN 978-4-04-604888-2)

この選手権が元になって、本も出版されています。元ネタの面白さの割に本の方はいまひとつな感じだったので、この記事は本の紹介カテゴリではなく雑談カテゴリに入れていますが、ちゃんと貸し出し対象なので読んでみたい方はご利用ください。私が大好きな「タテ切り」が収録されていないのがとても残念です。表彰作に入っていませんが「円錐をくり抜いて残りを2等分」というのも大好きです。

力技で積分を使うこともでき、円の面積は置換積分の例としてよく取り上げられますが、直接の不定積分も公式になっています。半径rの円の面積Sについて、上半分の面積を積分で書くと、積分定数をCとして、
S/2 = ∫{(r^2 - x^2)^(1/2)}dx
= 1/2{x(r^2 - x^2)^(1/2) + a^2*arcsin(x/r)} + C
となるので、ここに数値を入れてやれば計算機で面積を出せます。ほかに変わったものとして「とても細かく刻んで同じピース数に分ける」という手もあります。これは統計的な手法で、完全な等分はできませんが、どのピースを取るか無作為に決めるようにすれば、チャンスをほぼ平等にできます。ピースに余りが出た場合も、刻み方を細かくしておけば誤差の影響を無視できるでしょう。

ここまで見てきたように、中学数学の知識だけでなんとかする方法もありますが、決して簡単な問いではありません。ただ「3つに分ける」のに比べて「3等分」するのははるかに難しく、それを数学の問題として扱うなら「3等分できたと言える理由」も説明できなくてはならず、現実の問題として考えるなら「どうやって実行するか」まで問題になるので、なおさら大変です。さらには「正確さ」ではなく「公平さ」を追求する「公平分割問題」という考え方もあります。余談かつ私の私情ですが、元ネタの元ネタになった「すべてがゆがんで見えている」のコピーを書いた出版社の方にはぜひ「あなたは3等分できるんですか？」と聞いてみたいものです。

-関連記事-
図書貸出のお知らせ
-参考外部リンク-
【円を3等分する選手権表彰】数学クラスタにケーキを切らせるとこうなる
【円を3等分する選手権2表彰】数学クラスタにケーキを切らせるとこうなる。
ケーキの切れない非行少年たち@新潮社
著者インタビュー@ブックバン
ケーキを公平に分割するには？@NTTコミュニケーション科学基礎研究所

開店休業が続いているので、授業中に織り交ぜている小ネタを紹介してみます。もし日本語が母語でない読者がいたら、ぜひ挑戦してみてください。

シンプルなもの1
あんな残忍なことは誓ってもう一生しない。
[あんな ざんにんな ことは ちかって もういっしょう しない。]
(I'll never commit such a cruelties again for my whole life, I swear.)

シンプルなもの2
いい加減にしろと怒ったが、体のいい言い訳に言いくるめられた。
[いいがげんに しろと おこったが、ていのいい いいわけに いいくるめられた。]
(Though I was angry and said "It's enough", I was lulled into his plausible excuse.)

固有名詞1
高田馬場は高田早苗が馬場を開いた場所だというのは誤った話だ。
[たかだのばばは たかたさなえが ばばを ひらいた ばしょだ というのは あやまった はなしだ。]
(It is incorrect to say that Takadanobaba is the place where Takata Sanae established his riding ground.)

固有名詞2
庚さんと菅野重さんは生笹蒲鉾を勧めたが、笹さんと佐々さんはそそくさと立ち去った。
[かのえさんと　かんのえさんは　なまささかまぼこを　すすめたが、さささんと　さっささんは　そそくさと　たちさった。]
(Mr. Kanoe and Mrs. Kannoe offered Miss. Sasa and Mr. Sassa Nama-sasakamaboko, but they left hastily.)

専門用語1
部分分数分解は実体であって操作ではない。
[ぶぶんぶんすうぶんかいは じったいであって そうさではない。]
(A partial fractional decomposition is an entity, not an operation.)

専門用語2
可換環論と非可換環論の根本的な違いは、環の元が可換か非可換かという点にかかっている。つまり、可換環の元は演算に対し可換であるし、非可換環の元は演算に対し非可換である。
[かかんかんろんと ひかかんかんろんの こんぽんてきな ちがいは、かんの げんが かかんか ひかかんか というてんに かかっている。つまり、かかんかんの げんは えんざんに たいし かかんであるし、ひかかんかんの げんは えんざんに たいし ひかかんである。]
(The fundamental difference between commutative and non-commutative ring theory depends on whether the elements of the ring are commutative or non-commutative. In other words, the members of a commutative ring are commutative with respect to the operation, and the ones of a non-commutative ring are non-commutative with respect to the operation.)

余禄。日本人も発音しにくい、いわゆる早口言葉。
この竹垣に竹立てかけたのは竹立てかけたかったから竹立てかけた
私はこれが一番難しいと思います。

遠隔授業の増加でいわゆるデジタル教材のマーケットが広がり、文部科学省も昨年7月の資料（最終ページ）で義務教育の「学習者用デジタル教科書」を2024年度に本格導入する意向を発表しています。しかし今回紹介するのはそういった「新しい」デジタル教科書ではなく、ブロードバンドの黎明期から公開を続けている老舗の「電子」教科書です。

電子教科書（慶應義塾大学医学部解剖学教室編）
電子教科書で真っ先に思いつくのがこれです。私の勝手な思い入れですが、大学を卒業した後必要に迫られて解剖学を勉強したとき、それはそれはお世話になりました。今の時代にも残っているというだけで感慨深いです。現在はメタ・コーポレーション・ジャパンという企業がホストしているようです。

薬理学電子教科書
こちらは、開設した当初の様子しか知らなかったので、いつの間にか巨大な教科書に育っているのを見て、たいへんびっくりしました。理由はわかりませんが、医学や薬学の分野では、こういう情報公開が昔から盛んです。

福井研究室内の電子教科書
上の2つも無償で公開されている教科書ですが、福井先生の教科書はなんと、

このホームページにあるテキストのWord版の配布を始めました。またプログラムソースも配布しています。これらはすべて手を加えて再配布していただいて結構です。必要な方は以下のアドレスにメール（氏名と所属をお知らせ下さい）をお願いします。

という飛び切りの太っ腹です。徹底して実用的な数学の教科書で、数学が好きな生徒なら高校生でも十分独習できるものが半分くらいあります。

もちろん、ビジネスとしてのデジタル教材にも大いに盛り上がってもらわなくては困りますが、ずっと前からこういう取り組みを続けている方々のことも知っていただければと思い、たまたま私が思い出して探し当てられた3件を紹介しました。

-関連記事-
大学の先生のウェブサイト

タイトルは私の口癖みたいになっている言葉で、まなびやの生徒で聞いたことがない人はいないだろうと思います。ビデオに録り溜めてあった放送大学の授業を視聴していたところ、岸根先生の授業でほぼこれと同じ言葉が出てきて、我が意を得たりと嬉しくなったのでここで言いふらすことにしました。もとはファインマンの言葉なのだそうです。

-関連記事-
放送大学の授業と印刷教材

前回の記事から、写真撮影をウェブカメラの静止画機能からコンパクトデジタルカメラに変更しました。あまり変わった感じはしないかもしれませんが、撮影している本人としてはかなり鮮明さが増したつもりになっています。

これまでと勝手が異なるのが照明で、ウェブカメラは離れた場所に置いたまま使えましたが、デジカメは手で持って目で覗かないと撮影できないので、机の上の本を撮ろうとするとどうしても影ができます。するとフラッシュを焚くことになるのですが、光沢のある本だと全体に白っぽい雰囲気になりがちです。この辺の加減はどうしたものなのか、しばらく試行錯誤が必要そうです。

ちょっと前にsinc関数の極限の話題で高校数学の微積分の定義が少し甘いことに触れましたが、もっと素朴な問題もあります。

高校数学では、微分可能性についてはあんなにうるさく出題されるのに、積分可能性のことはほとんど聞かれません。なぜかというと、積分の定義がきちんとしていないから、もっとはっきりいえば「積分は微分の逆演算ではない」ということをスットボケたままだからです。例によって数学の先生による解説を紹介しましょう。

九州大学 原 隆 先生（数理物理学）による概論
名古屋大学大学院 浪川 幸彦 先生（モジュライ空間、数学教育）による説明
東京大学大学院 会田 茂樹 先生（確率論）による説明
個人的には「上積分と下積分の極限が一致するとき、その極限値」を定積分、不定積分は「aからbまでの定積分でbにxを代入したもの」としておけば、微分係数が「右極限と左極限が一致するとき、その極限値」で導関数が「f'(a)のaにxを代入したもの」であることとのバランスも取れるし、ずいぶんスッキリしそうに思います。積分区間が動くことがあるというのを受け入れておけば、いわゆる広義積分を特別扱いする必要もなくなりそうです。後で完全微分方程式の解法を習うときなども、この理解の方がスムーズかもしれません。

また、不定積分を先に求めないと定積分できないような定義をしていると、数学用語でいう「区分的に定義された」関数の扱いに困ります。たとえばy=|x|はx=0で微分できませんが、それ以外のすべての範囲で微分可能で「x<0のときy'=-1, x=0のとき微分不可能, x>0のときy'=1」ということになります。y'のグラフを描いてみればわかりますが、もし線分に面積がないのなら、この関数を積分（求積）できないというのはとても奇妙です。少なくとも「x=0を含まない区間の定積分」ができないと言い張るのは苦しすぎます。そのうえ、この関数を積分できないことにしておくためには、開区間は積分できないことにしなければなりません。それでいて「aからbまでの定積分＝aからcまでの定積分＋cからbまでの定積分」は正しいと習います。

この辺の事情を知っておくことで、高校数学のちょっとした取っ付きにくさ、ぎこちなさを、少し緩和できるのではないかと思います。

数学IIIで習う[sin(x)]/xについて、x→0の極限が1になることの説明に数学的な疑義がある、という問題があり、2013年度の大阪大学理系前期日程の第1問に出題されて有名になりました。この[sin(x)]/xは「カーディナルサイン関数」とか「非正規化sinc関数」などと呼ばれるもので、sincは「シンク」と発音する人と「ジンク」と発音する人がおり、一般に「sinc(x)」と書かれます。この問題に関する「インチキな」解法を思いついた、というのが今回の話題なのですが、その前に数学の先生によるちゃんとした説明を紹介しておきます。

関西学院大学　川中 宣明 先生（代数学）　による解説
宮城教育大学　瓜生 等 先生（微分方程式論）　による解決案
高知工科大学　井上 昌昭 先生（確率論）　による解決案
新潟工科大学　竹野 茂治 先生（双曲型保存則方程式）　による考察（PDF）
北海道大学　松本 圭司 先生（特殊関数論）による再構築案
難しい話も出てきますが、この問題は結局「円の面積はπr^2だと言ってよいかどうか（ちゃんと証明していないじゃないか）」という一点にかかっています。

私が思いついた解法にはcos(0)の微分係数を使います。まず原点が中心で半径1の円（単位円）を用意し、円周上に点A(1,0)と点B(cosθ,sinθ)を取ると、角AOBが偏角θをなし、弧ABの長さが弧度になります。ここで微分の定義に従って計算すると、cos'(0)=0すなわち「θ=0から微分小dθの増減があるときcosθは増減しない」が言えて、そのときの点Bが座標(1,sinθ)にあると見なしても誤差は無限に小さいことがわかります。弧ABとは円周上の点がAからBまで動いた軌跡なので「点Aからθが微分小の増減をするとき弧AB=θと線分AB=sinθが一致する」つまりθ→0のときθの極限とsinθの極限は等しく、ゆえにθ→0のとき[sin(θ)]/θ=1といえます。

この証明は厳密さを欠いており、すくなくとも「円の面積はπr^2だと証明もせずに言ってしまった」解答と同じくらい「ダメな」解答なのですが、しかしこれを「間違い」だと言ってしまうと矛盾を認めることになります。つまり、高校数学で習う範囲の微分の知識で本当に「接線が引ける」のなら、上の議論も正しいということになり、この証明が間違っているのだとすれば、高校数学の微分で接線を決定するのも誤りだということになります。微積分を厳密に定義しなければ、円の面積がπr^2だと言えないばかりか、接線を引くこともできない、とも言い換えられます。

大阪大学の受験生にこんな捻くれた回答をした人がいたのかどうか、知る方法はありませんが、もしいたとしたら何点もらえたのでしょうか。円の面積を証明なしで使った回答は、私の予想だと、満点ではないかもしれませんが、かなり高い得点をもらえたのではないかと思います。こうやって眺めてみる分には面白い問題ですが、円の面積を使って解いてから「これって証明できていないんじゃないか」と気付いた（おそらくは試験会場の中でもかなり優秀な）受験生が損をしたかもしれないと思えば、入学試験の問題としては少し配慮に欠けるところがあったかもしれません。