まなびやウェブログ

とくに高校生相手の相談で、進路を決めるということは、何年かの間「住む場所」を決めることでもある、ということをよく話します。もちろん、習得したい技能だとか必要になる費用だとか、他にもっと重要な事柄があるのは間違いありませんが、住む場所によって得られる経験というのも見過ごせない要素でしょう。

私個人としては、田舎の人には都会の暮らしを、都会の人には田舎の暮らしを体験してみて欲しいという願いがありますが、もっと大切なことはそれを「選ぶ」意識だと思っています。ずっと同じ場所で暮らすのだとしても、世の中に「ここ」とは違う場所があるらしいことを知ったうえで、自分で材料を得て選んだ結果であれば、そうでない場合とはおのずと違いが生まれてくるだろうという確信があります。

情報の伝達はどんどん速く容易になっていますが、一方でいろいろな分極が進んでいます。都会と田舎、若者と老人、金持ちと貧乏人、男性と女性、日本人と外国人、他にもまだまだあるでしょう。格差とか分断といった否定的な言葉が使われることもありますが、世の中が多様になれば、小さいグループで固まりたい心情が強くなるのは自然なことです。そういう傾向が進めば進むほど、高くなってしまった「隔たり」を越えなければならない機会も増えます。自分自身も「選んだ結果」として今ここにいるのだ、という認識がもしあれば、大きな助けになるに違いありません。

左上、右上、左下、右下の順に、Hamlet (The Oxford Shakespeare、2008年復刊本、1987初版)(ISBN 978-0-19-953581-1)、Hamlet (Oxford School Shakespeare、2007年改訂本)(ISBN 978-019-839906-3)、Hamlet (Cambridge School Shakespeare、Third edition)(ISBN 978-1-107-61548-9)、Hamlet, Prince of Denmark (The new cambridge shakespeare、Third edition)(ISBN 978-1-316-60673-5)
　
左から、ハムレット（福田訳）(ISBN 978-4-10-202003-6)、ハムレット（松岡訳）(ISBN 4-480-03301-7)、ハムレット（小田島訳）(ISBN 4-560-07023-7)、新訳 ハムレット（河合訳）(ISBN 978-4-04-210614-2)、ハムレットQ1（安西訳）(ISBN 978-4-334-75201-9)
　
シェイクスピアの紹介を始めたからには、触れないで済ませるわけにはいかない作品ですが、中身を解説するのは恐れ多いので、中身でないところについて書きます。中身の解説もしないのに写真の本の多さはいったい何なのか、という疑問はもっともですが、この「豊富さ」もハムレットの重要な特徴のひとつです。

イギリスにはオックスフォードとケンブリッジという名門大学があり、互いに対抗意識が強く、ことあるごとに張り合っていることで知られていますが、日本と違い出版分野でも両大学の出版局が大きな役割を果たしています。いっぽう、シェイクスピアというのはイギリスで一番有名な作家で、ハムレットはその一番有名な作品ですから、文学分野の出版物としてはもっとも大きな注目を集める看板商品になります。すると当然、オックスフォード大学出版局やケンブリッジ大学出版局が発行する「ハムレット」には、それぞれの英知と情熱と研究成果が惜しみなく注がれることになります。

ただし、オックスフォード版や新ケンブリッジ版のハムレットを読むのは、英文科の大学生にとっても簡単なことではありません。上演のための本であることを優先している新ケンブリッジ版に対して、オックスフォード版は文学研究を優先した構成で、読み進めるのはさらに大変です。最所先生の本を紹介した記事で「すぐには理解できなくても最高のものに触れてみよう」という話をしましたが、最初がこの2冊ではさすがに手ごわすぎるので、十二夜の紹介記事で触れたオックスフォード・スクール・シェイクスピアか、解説と本文が見開きで並んだケンブリッジ・スクール・シェイクスピアの方が無難です。

こちらがそのスクール・シェイクスピアの中身です。
　
左のオックスフォード版は徹底的な語注と視覚的なイメージを補うイラストが特徴です。単なる中高生向けバージョンを超えて、当時のビジュアルの資料として一級品のものが掲載されています。ケンブリッジ版は写真も含めカラー印刷されており、上演を強く意識した作りです。読者にテーマを与えて考えさせる（または話し合わせる）コーナーも豊富ですが、それでいて「勉強っぽい」感じになっていないのが巧妙です。どちらの本も、ひとつのジャンルの中で競い合いながら独自の方向性を持っていて、どちらも負けることなくそれぞれの主張を充実させ続けているのは、本当にお見事です。

-関連記事-
図書貸出のお知らせ
シェイクスピア関連の蔵書一覧
-参考外部リンク-
オックスフォード大学出版局
ケンブリッジ大学出版局

自分が悩んだときのメモを備忘録として公開しておきます。同じ問題で悩んでいる人以外にはまったく無意味な情報なのであしからず。

スタイルシートの記述をcssファイルで

a:link, a:visited {普通の設定;}
p#hoge a:link, a:visited {部分的な設定;}

としていたところ、chromeがページ全体に「部分的な設定」を適用してしまうという現象に遭遇した。試行錯誤の結果

a:link, a:visited {普通の設定;}
p#hoge a {部分的な設定;}

のように、ID決め打ちの部分には擬似クラスを指定しないことで解決した。

なぜ擬似クラスのところがカスケードせず上書きになってしまうのか不思議ですが、とりあえず上記で動いている様子。

リンクは記事の一番下にまとめておきましたが、ツイッター上で2年ちょっと前に開催された「丸いケーキを3等分する方法」を競うイベントの話題です。先に無難そうな回答例を紹介しておきましょう。小学生の知識でもできるやり方としては、内接正六角形を使うのが手っ取り早いでしょうか。

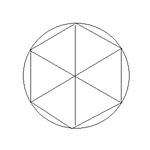
図はフリーハンドで描いているので不正確です。算数の範囲「だけ」で円の直径を引くには、ケーキの形をいったん紙に写して、半分折りにするくらいしかありませんが、天下り式の知識を使ってよいなら、定規を円周に当てて三角定規を接点に当てる、大きい三角定規の直角部分を円周に当てる、などの方法があります。中1で習う垂直二等分線の知識があれば、三角定規を使わず定木（長さを計れない直線を引けるだけの定規）とコンパスだけでOKです。直径さえわかれば、それを半分にすれば半径も中心もわかります。あとは、地道にやるなら正三角形を6つ作れば図のようになりますし、円周を半径と同じ長さの弦で6等分しても、結局同じことになります。直角の作り方は中1まで習いませんが、正三角形は小3で習うようです。

私が思いついたのは「4等分してから3等分」です。実は「直径を引いて、半径の垂直二等分線を引く」やり方の方が作業がスマートなのですが、それだと入賞作の「4等分線をイメージして切る」と結局同じになってしまいます。

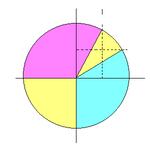
理屈としては、円を3等分する問題を扇形を3等分する問題に「落とし込んで」いるのがポイントで、こうやって切った方がきっと楽でしょう。この方法で数学的に正しい分割もできますが、ケーキを切る時にコンパスなんて使いたくないので、中心は目見当で適当に決め、直角も勘で切ります。もし自分の目の前に丸いケーキがあって、3等分しなければならなくなったら、きっとそうするだろうという確信があります。なお扇形を3等分するところは、算数の知識だけだと正三角形を作る（または分度器を使う）必要がありますが、sin(π/6) = cos(π/3) = 1/2がわかれば垂直二等分線で間に合います。中学校でルートを習うまで使えないsin(π/3) = cos(π/6) = {3^(1/2)}/2と違い、sin(π/6)は正三角形を半分にして長さを考えれば確認することができます。いわゆる「30-60の直角三角形」が、正三角形を2等分した図形であることは、覚えておくと少し得かもしれません。

数学クラスタが集まって本気で大喜利してみた(ISBN 978-4-04-604888-2)

この選手権が元になって、本も出版されています。元ネタの面白さの割に本の方はいまひとつな感じだったので、この記事は本の紹介カテゴリではなく雑談カテゴリに入れていますが、ちゃんと貸し出し対象なので読んでみたい方はご利用ください。私が大好きな「タテ切り」が収録されていないのがとても残念です。表彰作に入っていませんが「円錐をくり抜いて残りを2等分」というのも大好きです。

力技で積分を使うこともでき、円の面積は置換積分の例としてよく取り上げられますが、直接の不定積分も公式になっています。半径rの円の面積Sについて、上半分の面積を積分で書くと、積分定数をCとして、
S/2 = ∫{(r^2 - x^2)^(1/2)}dx
= 1/2{x(r^2 - x^2)^(1/2) + a^2*arcsin(x/r)} + C
となるので、ここに数値を入れてやれば計算機で面積を出せます。ほかに変わったものとして「とても細かく刻んで同じピース数に分ける」という手もあります。これは統計的な手法で、完全な等分はできませんが、どのピースを取るか無作為に決めるようにすれば、チャンスをほぼ平等にできます。ピースに余りが出た場合も、刻み方を細かくしておけば誤差の影響を無視できるでしょう。

ここまで見てきたように、中学数学の知識だけでなんとかする方法もありますが、決して簡単な問いではありません。ただ「3つに分ける」のに比べて「3等分」するのははるかに難しく、それを数学の問題として扱うなら「3等分できたと言える理由」も説明できなくてはならず、現実の問題として考えるなら「どうやって実行するか」まで問題になるので、なおさら大変です。さらには「正確さ」ではなく「公平さ」を追求する「公平分割問題」という考え方もあります。余談かつ私の私情ですが、元ネタの元ネタになった「すべてがゆがんで見えている」のコピーを書いた出版社の方にはぜひ「あなたは3等分できるんですか？」と聞いてみたいものです。

-関連記事-
図書貸出のお知らせ
-参考外部リンク-
【円を3等分する選手権表彰】数学クラスタにケーキを切らせるとこうなる
【円を3等分する選手権2表彰】数学クラスタにケーキを切らせるとこうなる。
ケーキの切れない非行少年たち@新潮社
著者インタビュー@ブックバン
ケーキを公平に分割するには？@NTTコミュニケーション科学基礎研究所