chromeがスタイルシートを読んでくれない対策
2021.12.06
自分が悩んだときのメモを備忘録として公開しておきます。同じ問題で悩んでいる人以外にはまったく無意味な情報なのであしからず。
スタイルシートの記述をcssファイルで
なぜ擬似クラスのところがカスケードせず上書きになってしまうのか不思議ですが、とりあえず上記で動いている様子。
スタイルシートの記述をcssファイルで
a:link, a:visited {普通の設定;}
p#hoge a:link, a:visited {部分的な設定;}a:link, a:visited {普通の設定;}
p#hoge a {部分的な設定;}なぜ擬似クラスのところがカスケードせず上書きになってしまうのか不思議ですが、とりあえず上記で動いている様子。
円を3等分する選手権
2021.12.06
リンクは記事の一番下にまとめておきましたが、ツイッター上で2年ちょっと前に開催された「丸いケーキを3等分する方法」を競うイベントの話題です。先に無難そうな回答例を紹介しておきましょう。小学生の知識でもできるやり方としては、内接正六角形を使うのが手っ取り早いでしょうか。
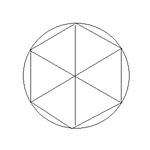
図はフリーハンドで描いているので不正確です。算数の範囲「だけ」で円の直径を引くには、ケーキの形をいったん紙に写して、半分折りにするくらいしかありませんが、天下り式の知識を使ってよいなら、定規を円周に当てて三角定規を接点に当てる、大きい三角定規の直角部分を円周に当てる、などの方法があります。中1で習う垂直二等分線の知識があれば、三角定規を使わず定木(長さを計れない直線を引けるだけの定規)とコンパスだけでOKです。直径さえわかれば、それを半分にすれば半径も中心もわかります。あとは、地道にやるなら正三角形を6つ作れば図のようになりますし、円周を半径と同じ長さの弦で6等分しても、結局同じことになります。直角の作り方は中1まで習いませんが、正三角形は小3で習うようです。
私が思いついたのは「4等分してから3等分」です。実は「直径を引いて、半径の垂直二等分線を引く」やり方の方が作業がスマートなのですが、それだと入賞作の「4等分線をイメージして切る」と結局同じになってしまいます。
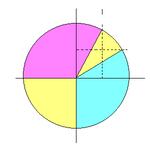
理屈としては、円を3等分する問題を扇形を3等分する問題に「落とし込んで」いるのがポイントで、こうやって切った方がきっと楽でしょう。この方法で数学的に正しい分割もできますが、ケーキを切る時にコンパスなんて使いたくないので、中心は目見当で適当に決め、直角も勘で切ります。もし自分の目の前に丸いケーキがあって、3等分しなければならなくなったら、きっとそうするだろうという確信があります。なお扇形を3等分するところは、算数の知識だけだと正三角形を作る(または分度器を使う)必要がありますが、sin(π/6) = cos(π/3) = 1/2がわかれば垂直二等分線で間に合います。中学校でルートを習うまで使えないsin(π/3) = cos(π/6) = {3^(1/2)}/2と違い、sin(π/6)は正三角形を半分にして長さを考えれば確認することができます。いわゆる「30-60の直角三角形」が、正三角形を2等分した図形であることは、覚えておくと少し得かもしれません。
数学クラスタが集まって本気で大喜利してみた(ISBN 978-4-04-604888-2)

この選手権が元になって、本も出版されています。元ネタの面白さの割に本の方はいまひとつな感じだったので、この記事は本の紹介カテゴリではなく雑談カテゴリに入れていますが、ちゃんと貸し出し対象なので読んでみたい方はご利用ください。私が大好きな「タテ切り」が収録されていないのがとても残念です。表彰作に入っていませんが「円錐をくり抜いて残りを2等分」というのも大好きです。
力技で積分を使うこともでき、円の面積は置換積分の例としてよく取り上げられますが、直接の不定積分も公式になっています。半径rの円の面積Sについて、上半分の面積を積分で書くと、積分定数をCとして、
S/2 = ∫{(r^2 - x^2)^(1/2)}dx
= 1/2{x(r^2 - x^2)^(1/2) + a^2*arcsin(x/r)} + C
となるので、ここに数値を入れてやれば計算機で面積を出せます。ほかに変わったものとして「とても細かく刻んで同じピース数に分ける」という手もあります。これは統計的な手法で、完全な等分はできませんが、どのピースを取るか無作為に決めるようにすれば、チャンスをほぼ平等にできます。ピースに余りが出た場合も、刻み方を細かくしておけば誤差の影響を無視できるでしょう。
ここまで見てきたように、中学数学の知識だけでなんとかする方法もありますが、決して簡単な問いではありません。ただ「3つに分ける」のに比べて「3等分」するのははるかに難しく、それを数学の問題として扱うなら「3等分できたと言える理由」も説明できなくてはならず、現実の問題として考えるなら「どうやって実行するか」まで問題になるので、なおさら大変です。さらには「正確さ」ではなく「公平さ」を追求する「公平分割問題」という考え方もあります。余談かつ私の私情ですが、元ネタの元ネタになった「すべてがゆがんで見えている」のコピーを書いた出版社の方にはぜひ「あなたは3等分できるんですか?」と聞いてみたいものです。
-関連記事-
図書貸出のお知らせ
-参考外部リンク-
【円を3等分する選手権表彰】数学クラスタにケーキを切らせるとこうなる
【円を3等分する選手権2表彰】数学クラスタにケーキを切らせるとこうなる。
ケーキの切れない非行少年たち@新潮社
著者インタビュー@ブックバン
ケーキを公平に分割するには?@NTTコミュニケーション科学基礎研究所

図はフリーハンドで描いているので不正確です。算数の範囲「だけ」で円の直径を引くには、ケーキの形をいったん紙に写して、半分折りにするくらいしかありませんが、天下り式の知識を使ってよいなら、定規を円周に当てて三角定規を接点に当てる、大きい三角定規の直角部分を円周に当てる、などの方法があります。中1で習う垂直二等分線の知識があれば、三角定規を使わず定木(長さを計れない直線を引けるだけの定規)とコンパスだけでOKです。直径さえわかれば、それを半分にすれば半径も中心もわかります。あとは、地道にやるなら正三角形を6つ作れば図のようになりますし、円周を半径と同じ長さの弦で6等分しても、結局同じことになります。直角の作り方は中1まで習いませんが、正三角形は小3で習うようです。
私が思いついたのは「4等分してから3等分」です。実は「直径を引いて、半径の垂直二等分線を引く」やり方の方が作業がスマートなのですが、それだと入賞作の「4等分線をイメージして切る」と結局同じになってしまいます。

理屈としては、円を3等分する問題を扇形を3等分する問題に「落とし込んで」いるのがポイントで、こうやって切った方がきっと楽でしょう。この方法で数学的に正しい分割もできますが、ケーキを切る時にコンパスなんて使いたくないので、中心は目見当で適当に決め、直角も勘で切ります。もし自分の目の前に丸いケーキがあって、3等分しなければならなくなったら、きっとそうするだろうという確信があります。なお扇形を3等分するところは、算数の知識だけだと正三角形を作る(または分度器を使う)必要がありますが、sin(π/6) = cos(π/3) = 1/2がわかれば垂直二等分線で間に合います。中学校でルートを習うまで使えないsin(π/3) = cos(π/6) = {3^(1/2)}/2と違い、sin(π/6)は正三角形を半分にして長さを考えれば確認することができます。いわゆる「30-60の直角三角形」が、正三角形を2等分した図形であることは、覚えておくと少し得かもしれません。
数学クラスタが集まって本気で大喜利してみた(ISBN 978-4-04-604888-2)

この選手権が元になって、本も出版されています。元ネタの面白さの割に本の方はいまひとつな感じだったので、この記事は本の紹介カテゴリではなく雑談カテゴリに入れていますが、ちゃんと貸し出し対象なので読んでみたい方はご利用ください。私が大好きな「タテ切り」が収録されていないのがとても残念です。表彰作に入っていませんが「円錐をくり抜いて残りを2等分」というのも大好きです。
力技で積分を使うこともでき、円の面積は置換積分の例としてよく取り上げられますが、直接の不定積分も公式になっています。半径rの円の面積Sについて、上半分の面積を積分で書くと、積分定数をCとして、
S/2 = ∫{(r^2 - x^2)^(1/2)}dx
= 1/2{x(r^2 - x^2)^(1/2) + a^2*arcsin(x/r)} + C
となるので、ここに数値を入れてやれば計算機で面積を出せます。ほかに変わったものとして「とても細かく刻んで同じピース数に分ける」という手もあります。これは統計的な手法で、完全な等分はできませんが、どのピースを取るか無作為に決めるようにすれば、チャンスをほぼ平等にできます。ピースに余りが出た場合も、刻み方を細かくしておけば誤差の影響を無視できるでしょう。
ここまで見てきたように、中学数学の知識だけでなんとかする方法もありますが、決して簡単な問いではありません。ただ「3つに分ける」のに比べて「3等分」するのははるかに難しく、それを数学の問題として扱うなら「3等分できたと言える理由」も説明できなくてはならず、現実の問題として考えるなら「どうやって実行するか」まで問題になるので、なおさら大変です。さらには「正確さ」ではなく「公平さ」を追求する「公平分割問題」という考え方もあります。余談かつ私の私情ですが、元ネタの元ネタになった「すべてがゆがんで見えている」のコピーを書いた出版社の方にはぜひ「あなたは3等分できるんですか?」と聞いてみたいものです。
-関連記事-
図書貸出のお知らせ
-参考外部リンク-
【円を3等分する選手権表彰】数学クラスタにケーキを切らせるとこうなる
【円を3等分する選手権2表彰】数学クラスタにケーキを切らせるとこうなる。
ケーキの切れない非行少年たち@新潮社
著者インタビュー@ブックバン
ケーキを公平に分割するには?@NTTコミュニケーション科学基礎研究所
 2021.12.06 16:45
|
2021.12.06 16:45
| 

