なぜどのように「わからなく」なるか 後編
2021.10.09
前編からの続きです。
ここで苦労する生徒は、大きく2パターンに分かれます。いっぽうは、教室でやり方を習ったときには問題が解けたのに、しばらく後で同じ質問をするとまた同じところで止まってしまうタイプです。こういう生徒は、決してやる気がないわけでも記憶力が悪いわけでもなく、自分の担当範囲が「計算作業だけ」だと信じ切っている場合がほとんどです。先生に「こうやって解きなさい」と指示されるのを、当然のことのように待っています。この誤解を解くのは大変で、本人が「自分は正当に努力しているのに不当な要求をされている」と感じてしまわないよう、十分配慮しなければなりません。
もうひとつ注意が必要なのは、この「指示待ち」姿勢が単純に悪いものではなく、指示を待てるというのはひとつの能力だということです。問題は、普通の生活の中で「待つ」と「待たない」の両方がある程度は求められ、たいていはその使い分けを自分でやる必要があることです。たとえば仕事をするにしても、どんなときも指示されたこと以外絶対してはならないというのは、よほどの危険を伴う業務に限られるでしょうが、いつでも指示を待たずに行動できるのがよいという職種も多くはないでしょう。その判断をするために、両方に習熟してメリットとデメリットを比較できれば理想的ですが、少なくとも両方を経験しておく必要はあるでしょう。本格的に「数学を使う」仕事に就く人はごく少数なのに、中学校で全員が数学を習うのは、こういう問題となるべく早い時期に向き合っておくためでもあります。
もういっぽうは後戻りができないタイプで、算数の練習量が多かった生徒に多く見受けられます。中学入学くらいまでの成績は優秀で、解き方を自分で探ろうとする意識も持っていることがほとんどですが、いったん自分が「心地よい」やり方を発見すると、見直したり修正したりといったことができなくなりがちです。より効率のよいやり方を教わっても、理屈をつけて自分のやり方を守ろうとします。この「理屈をつける」部分が素直に丁寧に行われる分には、よく考えて納得してからやり方を変えるという美徳になりますが、どう考えても今までのやり方では不足なようだと知ってなお後戻りができないときには、勉強や努力自体に否定的な態度になってしまうこともあります。
専門的にどのように評価されているのか知りませんが私の経験上、成績に響いてくるようになるタイミングに性差があり、男子生徒では中学3年から高校1年くらい、女子生徒では高校2年から3年くらいが典型的です。出口となる考え方には2面あり、学習に限らず生活全般で「心地よさ」を過剰に求めないで済むような配慮と、年齢相応に「どう理屈をつけても現実になんとかする以外ない問題」に向き合うような促しが、どちらも重要です。余談ながら、私が通っていた当時の予備校はまさに後者の一本槍で、冷徹に「今年が去年と同じなら、来年も今年と同じだよ」と言われて大きく伸びた生徒も、挫けてしまった生徒も、両方たくさんいました。私自身は「今やりたくないことがあるなら、やってもいいなと思うことを先にやって、少し経験を積んでから考えた方が得だろう」という考えで、本人に強い希望がある場合を除き、本当に難しいことは先送りと再挑戦を繰り返すよう心がけています。
ここで苦労する生徒は、大きく2パターンに分かれます。いっぽうは、教室でやり方を習ったときには問題が解けたのに、しばらく後で同じ質問をするとまた同じところで止まってしまうタイプです。こういう生徒は、決してやる気がないわけでも記憶力が悪いわけでもなく、自分の担当範囲が「計算作業だけ」だと信じ切っている場合がほとんどです。先生に「こうやって解きなさい」と指示されるのを、当然のことのように待っています。この誤解を解くのは大変で、本人が「自分は正当に努力しているのに不当な要求をされている」と感じてしまわないよう、十分配慮しなければなりません。
もうひとつ注意が必要なのは、この「指示待ち」姿勢が単純に悪いものではなく、指示を待てるというのはひとつの能力だということです。問題は、普通の生活の中で「待つ」と「待たない」の両方がある程度は求められ、たいていはその使い分けを自分でやる必要があることです。たとえば仕事をするにしても、どんなときも指示されたこと以外絶対してはならないというのは、よほどの危険を伴う業務に限られるでしょうが、いつでも指示を待たずに行動できるのがよいという職種も多くはないでしょう。その判断をするために、両方に習熟してメリットとデメリットを比較できれば理想的ですが、少なくとも両方を経験しておく必要はあるでしょう。本格的に「数学を使う」仕事に就く人はごく少数なのに、中学校で全員が数学を習うのは、こういう問題となるべく早い時期に向き合っておくためでもあります。
もういっぽうは後戻りができないタイプで、算数の練習量が多かった生徒に多く見受けられます。中学入学くらいまでの成績は優秀で、解き方を自分で探ろうとする意識も持っていることがほとんどですが、いったん自分が「心地よい」やり方を発見すると、見直したり修正したりといったことができなくなりがちです。より効率のよいやり方を教わっても、理屈をつけて自分のやり方を守ろうとします。この「理屈をつける」部分が素直に丁寧に行われる分には、よく考えて納得してからやり方を変えるという美徳になりますが、どう考えても今までのやり方では不足なようだと知ってなお後戻りができないときには、勉強や努力自体に否定的な態度になってしまうこともあります。
専門的にどのように評価されているのか知りませんが私の経験上、成績に響いてくるようになるタイミングに性差があり、男子生徒では中学3年から高校1年くらい、女子生徒では高校2年から3年くらいが典型的です。出口となる考え方には2面あり、学習に限らず生活全般で「心地よさ」を過剰に求めないで済むような配慮と、年齢相応に「どう理屈をつけても現実になんとかする以外ない問題」に向き合うような促しが、どちらも重要です。余談ながら、私が通っていた当時の予備校はまさに後者の一本槍で、冷徹に「今年が去年と同じなら、来年も今年と同じだよ」と言われて大きく伸びた生徒も、挫けてしまった生徒も、両方たくさんいました。私自身は「今やりたくないことがあるなら、やってもいいなと思うことを先にやって、少し経験を積んでから考えた方が得だろう」という考えで、本人に強い希望がある場合を除き、本当に難しいことは先送りと再挑戦を繰り返すよう心がけています。
なぜどのように「わからなく」なるか 前編
2021.10.09
まなびやでは、たとえ受験科目に数学がない大学受験生であっても、時間が許せば最初に数学の授業をしている、という話を以前少し書きました。その中でもとくに重要なのがこれです。

問題自体は、中学生でもほとんどの生徒が解けます。
しかし大切なのは、生徒の頭の中で問題がどう扱われたかです。素朴に「aが2つとaが3つだから、合わせるとaは5つ」と考えても正しい答えが出ます。
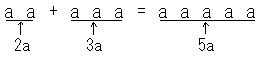
この理解は便利なようですが、実は大きな落とし穴があります。
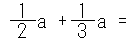
たとえばこの問題が解けません。分数くらいなら頭の中で解決できる力自慢がいるかもしれませんが、π(円周率)やe(ネイピア数)のような無理数だとか、単に文字でxとかyとか言われた場合には対応できなくなります。
より使い回しが広い理解は、たとえばこのようなものです。
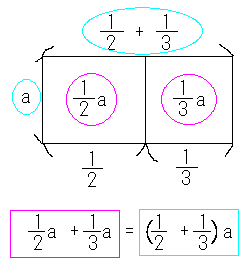
微積分が登場するまでの間は「掛け算は面積、面積は掛け算」だけで押し切れるので、いわゆる「同類項」は「高さが同じだから横に並べられる長方形」と同義だと見て大丈夫です。
これさえ覚えて帰ればいいだけなので、何の問題もないように見えます。しかし実際は、一筋縄ではありません。後編に続きます。

問題自体は、中学生でもほとんどの生徒が解けます。
しかし大切なのは、生徒の頭の中で問題がどう扱われたかです。素朴に「aが2つとaが3つだから、合わせるとaは5つ」と考えても正しい答えが出ます。
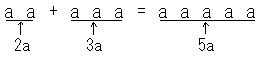
この理解は便利なようですが、実は大きな落とし穴があります。
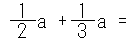
たとえばこの問題が解けません。分数くらいなら頭の中で解決できる力自慢がいるかもしれませんが、π(円周率)やe(ネイピア数)のような無理数だとか、単に文字でxとかyとか言われた場合には対応できなくなります。
より使い回しが広い理解は、たとえばこのようなものです。

微積分が登場するまでの間は「掛け算は面積、面積は掛け算」だけで押し切れるので、いわゆる「同類項」は「高さが同じだから横に並べられる長方形」と同義だと見て大丈夫です。
これさえ覚えて帰ればいいだけなので、何の問題もないように見えます。しかし実際は、一筋縄ではありません。後編に続きます。
 2021.10.09 20:02
|
2021.10.09 20:02
| 

