書籍以外の教材
2021.06.28
左から、タコ糸、トランプ、地球儀。

まなびやの生徒なら誰でも見た瞬間に「いつものアレか」とわかってしまう、お馴染みの小物たちです。
タコ糸は、ホワイトボードマーカーのカスがついた手で扱うのですっかり黒ずんでいますが、立体に紐を巻きつける問題を実演したり、ワリバシと組み合わせて図形の辺や線分に見立てたり、ときにはセロテープの芯に巻き付けて滑車を再現したり、意外と活躍してくれます。トランプはもっぱら数学用で、場合の数の授業には欠かせません。順列も組み合わせもこれでバッチリです。地球儀はもちろん地理の説明に使いますが、気象や天体など理科の授業でも役立ちます。地球が丸いことを考慮しないと理解できない事柄は多くあり、頭の中だけで立体を把握するのは難しいため、できるなら家庭学習でも活用して欲しい教材です。
わざわざ写真撮影はしませんでしたが、上の3点よりさらに重要なのが紙です。まなびやで用意しているのは単なるA4のコピー用紙ですが、生徒が自分で持ってきたノートとは別に、この「綴じられていない無地の紙」があると、この上なく便利なのです。今の生徒はとにかく「下書きができない」傾向が強く、長くなりそうな枝葉の計算を別の紙で片付けるとか、文章の要点をメモしながら読み進めるとか、出てきた数字を図や表にまとめておくといった工夫が、なかなか身に付きません。解決法は慣れと根気しかなく、まなびやの教室では「頭を使って悩むより手を使って紙に書こう」が合言葉のように繰り返されています。

まなびやの生徒なら誰でも見た瞬間に「いつものアレか」とわかってしまう、お馴染みの小物たちです。
タコ糸は、ホワイトボードマーカーのカスがついた手で扱うのですっかり黒ずんでいますが、立体に紐を巻きつける問題を実演したり、ワリバシと組み合わせて図形の辺や線分に見立てたり、ときにはセロテープの芯に巻き付けて滑車を再現したり、意外と活躍してくれます。トランプはもっぱら数学用で、場合の数の授業には欠かせません。順列も組み合わせもこれでバッチリです。地球儀はもちろん地理の説明に使いますが、気象や天体など理科の授業でも役立ちます。地球が丸いことを考慮しないと理解できない事柄は多くあり、頭の中だけで立体を把握するのは難しいため、できるなら家庭学習でも活用して欲しい教材です。
わざわざ写真撮影はしませんでしたが、上の3点よりさらに重要なのが紙です。まなびやで用意しているのは単なるA4のコピー用紙ですが、生徒が自分で持ってきたノートとは別に、この「綴じられていない無地の紙」があると、この上なく便利なのです。今の生徒はとにかく「下書きができない」傾向が強く、長くなりそうな枝葉の計算を別の紙で片付けるとか、文章の要点をメモしながら読み進めるとか、出てきた数字を図や表にまとめておくといった工夫が、なかなか身に付きません。解決法は慣れと根気しかなく、まなびやの教室では「頭を使って悩むより手を使って紙に書こう」が合言葉のように繰り返されています。
マルケスとフォークナー
2021.06.25
左から、予告された殺人の記録(ISBN 978-4-10-205211-2)、エレンディラ(ISBN 4-480-02277-5)


南米文学といえばこのマルケス調というくらい流行した、ガルシア=マルケスの中編と短編集です。この著者の作品としては「百年の孤独」の方が有名ですが、何年も前に手放してしまって以来、買い戻す機会に恵まれていません。文庫版がなくやや高価なので、古本屋で見つけても「もう少し安く出ることがあるかも」と、セコい考えに押し切られてしまいます。
フォークナー短編集(ISBN 978-4-10-210203-9)

フォークナーはマルケスよりも30年くらい前の人で、作品を埋め尽くす閉塞感や翻弄感がどこか似ています。思えば、日本にとってもっとも親しい国であるはずなのに、私たちはアメリカの歴史や社会についてあまり大きな関心を払っていません。フォークナーを読めばアメリカがわかる、というのはちょっと短絡的すぎますが、アメリカを知りたい人が前もって読んでおくには格好の作家です。
3冊ともかなり「刺激が強い」本で、残酷な描写も遠慮なく出てきます。私も高校生に勧めようとは思いませんが、年を取りすぎるとこういう異質さに溢れた世界を見る目が鈍くなってくるので、大学生くらいの時期に読むのがちょうどいいのかなと思います。フォークナーは50年、マルケスは82年にノーベル文学賞を受賞した大作家なので、いまさら私が褒めても何の足しにもなりませんが、彼らのように「伝えるべきもの」を持った作家の力強さには、驚嘆しかありません。
-関連記事-
図書貸出のお知らせ


南米文学といえばこのマルケス調というくらい流行した、ガルシア=マルケスの中編と短編集です。この著者の作品としては「百年の孤独」の方が有名ですが、何年も前に手放してしまって以来、買い戻す機会に恵まれていません。文庫版がなくやや高価なので、古本屋で見つけても「もう少し安く出ることがあるかも」と、セコい考えに押し切られてしまいます。
フォークナー短編集(ISBN 978-4-10-210203-9)

フォークナーはマルケスよりも30年くらい前の人で、作品を埋め尽くす閉塞感や翻弄感がどこか似ています。思えば、日本にとってもっとも親しい国であるはずなのに、私たちはアメリカの歴史や社会についてあまり大きな関心を払っていません。フォークナーを読めばアメリカがわかる、というのはちょっと短絡的すぎますが、アメリカを知りたい人が前もって読んでおくには格好の作家です。
3冊ともかなり「刺激が強い」本で、残酷な描写も遠慮なく出てきます。私も高校生に勧めようとは思いませんが、年を取りすぎるとこういう異質さに溢れた世界を見る目が鈍くなってくるので、大学生くらいの時期に読むのがちょうどいいのかなと思います。フォークナーは50年、マルケスは82年にノーベル文学賞を受賞した大作家なので、いまさら私が褒めても何の足しにもなりませんが、彼らのように「伝えるべきもの」を持った作家の力強さには、驚嘆しかありません。
-関連記事-
図書貸出のお知らせ
勉強中の数学メモ3
2021.05.22
ピアソンのカイ2乗検定とフィッシャーの直接確率検定では、帰無仮説が異なる。カイ2乗検定の帰無仮説は平均効果が0であるというもので、プラスの効果とマイナスの効果が同確率で同程度に現れる場合は棄却されない。直接確率検定の帰無仮説は個体効果が0であるというもので、プラスの効果もマイナスの効果もない場合にのみ棄却されない。後者の方が強い条件であり「シャープな帰無仮説」と呼ばれる。カイ2乗検定にイェーツの連続性補正を施すと、直接確率検定の結果とよく近似するようになる。「フィッシャー検定」という呼称も一般的ではあるが、F検定と紛らわしい。カイ2乗検定は復元抽出の分布である二項分布に、直接確率検定は非復元抽出の分布である超幾何分布に基づく、らしいのだが二項分布からカイ2乗分布に乗り換える必然性がいまひとつピンとこない。追記:二項分布や超幾何分布は大標本で計算量が大きく増えることが大きな理由。標本が大きければカイ2乗分布で代用する誤差は小さく、自由度の扱いなど計算量以外にもメリットがある。
独立二群の平均値差に関するスチューデントのt検定とウェルチのt検定は、どちらも母集団が正規分布することを前提とするが、前者がさらに等分散を要求するのに対し、後者は非等分散であってもよいように補正してある。検定の多重性を避けるために、等分散であることが自明でないデータであればウェルチのt検定を用いるべき。F検定は正規分布に従う2つの群の標準偏差が等しいかどうか、正規分布に従い標準偏差が等しい2つの群の平均が等しいかどうか、のどちらか(だけ)に用いるのが無難。t検定の前に、KS検定などを行って前提の適合度を評価するのは差し支えない。
余談ながら、ディラックのデルタを正規分布関数の極限で近似する手法を調べていたときに、岡竜之介のブログという愉快なウェブログを発見したので紹介します。ディラックのデルタに対抗して「イプシロン」なる変な関数を勝手に、しかし真面目に作ってしまった話だとか、算数の問題を作るとき先生が密かにイラっとしている「通分して計算したら約分が必要なくなってしまう問題」をスッキリ解決するプログラムを作る話だとかが、どこか昔懐かしいテイストとともに掲載されています。数学IIIまで勉強した生徒なら、少し背伸びすれば面白おかしく読めると思います。
-シリーズリンク-
前のメモ<>次のメモ
独立二群の平均値差に関するスチューデントのt検定とウェルチのt検定は、どちらも母集団が正規分布することを前提とするが、前者がさらに等分散を要求するのに対し、後者は非等分散であってもよいように補正してある。検定の多重性を避けるために、等分散であることが自明でないデータであればウェルチのt検定を用いるべき。F検定は正規分布に従う2つの群の標準偏差が等しいかどうか、正規分布に従い標準偏差が等しい2つの群の平均が等しいかどうか、のどちらか(だけ)に用いるのが無難。t検定の前に、KS検定などを行って前提の適合度を評価するのは差し支えない。
余談ながら、ディラックのデルタを正規分布関数の極限で近似する手法を調べていたときに、岡竜之介のブログという愉快なウェブログを発見したので紹介します。ディラックのデルタに対抗して「イプシロン」なる変な関数を勝手に、しかし真面目に作ってしまった話だとか、算数の問題を作るとき先生が密かにイラっとしている「通分して計算したら約分が必要なくなってしまう問題」をスッキリ解決するプログラムを作る話だとかが、どこか昔懐かしいテイストとともに掲載されています。数学IIIまで勉強した生徒なら、少し背伸びすれば面白おかしく読めると思います。
-シリーズリンク-
前のメモ<>次のメモ
勉強中の数学メモ2
2021.05.22
イプシロンデルタ論法は一見面倒そうだが、ようするに、高校数学でいう「Δx」を無限に小さく「できることを保証」するための方法論である。
微分をライプニッツの記法で書いたときのdy/dxはもともと「Δy/ΔxについてΔx→0の極限を取ろう」という意図で、次元を意識しないときは「微分小」とか「無限小変分」などと呼ばれる。これを正確に理解するには外微分の知識が必要になり、本格的な数学にほんの少しだけ足を突っ込むことになってしまい、それはそれは恐ろしく大変なことになる。どうしても知りたい人は下記を参照。
http://www.math.titech.ac.jp/~kawahira/courses/kiso.html
http://sshmathgeom.private.coocan.jp/diffgeom/tangentvec.pdf
https://www.math.sci.hokudai.ac.jp/~ishikawa/kikaA08/08-kikaA-hosoku2.pdf
全微分(ないし一次微分形式)をこのように書く、という知識のところで立ち止まるのも方便ではないか。
高校範囲の知識でなんとなくのイメージが得られないか、と考えてみたところ、多変数関数を扱うときに意味が出てくる概念なのだから、変数を増やせばよさそう。ということで媒介変数関数の微分公式をイメージするのはどうだろうか。x=f(t)かつy=g(t)ならばdy/dx=g'(t)/g'(t)というアレである。ライプニッツの記法とラグランジュの記法を混ぜて書くのは奇妙だが、こうすると「dx=g'(t)なのかな」というイメージが、なんとなく沸いてくるような気がする。またyをxで2階微分するのをライプニッツの記法でd^2y/dx^2と書くが、これはd(dy/dx)/dxという風に繁分数で書いた方が誤解が少ないのではないか。こうしておけば、媒介変数表示でdy/dx=h(t)=g'(t)/g'(t)となっているときのd(dy/dx)/dx=[d(dy/dy)/dt]*[dt/dx]なんかも、より自然に理解できるように思う。
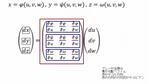
n個の変数X=(x1,x2...,xn)が像F=(f1,f2...,fm)をなし(どちらも列ベクトルとして考える)、すべてのfiがxjで偏微分可能なとき、i行j列が∂fi/∂xjとなる行列を、多変数ベクトル値関数Fのヤコビ行列という。全微分を与える表現行列だと見ることもできるし、Fの要素の勾配ベクトルを行として縦に積み上げたと見ることもできる。
-シリーズリンク-
前のメモ<>次のメモ
微分をライプニッツの記法で書いたときのdy/dxはもともと「Δy/ΔxについてΔx→0の極限を取ろう」という意図で、次元を意識しないときは「微分小」とか「無限小変分」などと呼ばれる。これを正確に理解するには外微分の知識が必要になり、本格的な数学にほんの少しだけ足を突っ込むことになってしまい、それはそれは恐ろしく大変なことになる。どうしても知りたい人は下記を参照。
http://www.math.titech.ac.jp/~kawahira/courses/kiso.html
http://sshmathgeom.private.coocan.jp/diffgeom/tangentvec.pdf
https://www.math.sci.hokudai.ac.jp/~ishikawa/kikaA08/08-kikaA-hosoku2.pdf
全微分(ないし一次微分形式)をこのように書く、という知識のところで立ち止まるのも方便ではないか。
高校範囲の知識でなんとなくのイメージが得られないか、と考えてみたところ、多変数関数を扱うときに意味が出てくる概念なのだから、変数を増やせばよさそう。ということで媒介変数関数の微分公式をイメージするのはどうだろうか。x=f(t)かつy=g(t)ならばdy/dx=g'(t)/g'(t)というアレである。ライプニッツの記法とラグランジュの記法を混ぜて書くのは奇妙だが、こうすると「dx=g'(t)なのかな」というイメージが、なんとなく沸いてくるような気がする。またyをxで2階微分するのをライプニッツの記法でd^2y/dx^2と書くが、これはd(dy/dx)/dxという風に繁分数で書いた方が誤解が少ないのではないか。こうしておけば、媒介変数表示でdy/dx=h(t)=g'(t)/g'(t)となっているときのd(dy/dx)/dx=[d(dy/dy)/dt]*[dt/dx]なんかも、より自然に理解できるように思う。

n個の変数X=(x1,x2...,xn)が像F=(f1,f2...,fm)をなし(どちらも列ベクトルとして考える)、すべてのfiがxjで偏微分可能なとき、i行j列が∂fi/∂xjとなる行列を、多変数ベクトル値関数Fのヤコビ行列という。全微分を与える表現行列だと見ることもできるし、Fの要素の勾配ベクトルを行として縦に積み上げたと見ることもできる。
-シリーズリンク-
前のメモ<>次のメモ
勉強中の数学メモ1
2021.05.22
このところ少し数学の勉強をしていて、備忘録的にメモっておいたことや、なんとなく思いついたことなどを書き溜めるうちにけっこうな分量になったので、物の役には立たないでしょうが公開してみます。あくまで勉強中のメモで、どの程度正しい理解なのか私は知りません。
Aを行列、xとbを列ベクトルとして
A*x=bならば
A^-1*A*x=A^-1*b
x=A^-1*b
という演算ができる。線型方程式がn個の変数を持ちn本の一次方程式からなるとき、それらを行列表示したものをAとすると正方行列になるが、Aが正則である(逆行列をもつ)ならば、ベクトルxのi番目の成分xiは、Aのi列をbに置き換えた行列をAiとして、
xi=det(Ai)/det(A)
と一意に解くことができ、クラメールの規則とかクラメルの公式などと呼ばれる。
A^-1を求めるとき、実用上は掃き出し法などの方が計算量の増加が穏やかだが、余因子展開の方が原理がわかりやすい。Aのi行めとj列めを除いた行列をAijと書き、余因子Δijを
Δij=(−1)^(i+j)*det(Aij)
と定義する。この余因子を要素とするi行j列の行列をA^(流儀によってはC)、それを転置したものをA~(余因子行列)として、ライプニッツの明示公式から行列式の多重線型性を確認すれば、
A^-1=(1/det(A))*A~
が成り立つことがわかる。
n個の関数(実関数でも複素関数でもよい)f1,f2...,fnが区間I上でn−1階微分可能とするとき、f1の0~n-1階微分を縦に並べた列ベクトルf1(x),f2の0~n-1階微分を縦に並べた列ベクトルf2(x)...,fnの0~n-1階微分を縦に並べた列ベクトルfn(x)を横に並べて作った行列(i行j列成分が、fjのi-1階微分になる)の行列式をロンスキー行列式W(f1,f2...,fn)という。ロンスキー行列式(ロンスキアン)が「恒等的に0」でないとき、f1,f2...,fnからなる関数族は線形独立な解をもつ。厳密な証明はさておき、拡大係数行列で連立方程式を解く操作を確認すれば、おそらくそうなのだという納得はできよう。関数族が線形従属である条件は難しいようで、ペアノなどが考察を与えているらしい。
-シリーズリンク-
次のメモ
Aを行列、xとbを列ベクトルとして
A*x=bならば
A^-1*A*x=A^-1*b
x=A^-1*b
という演算ができる。線型方程式がn個の変数を持ちn本の一次方程式からなるとき、それらを行列表示したものをAとすると正方行列になるが、Aが正則である(逆行列をもつ)ならば、ベクトルxのi番目の成分xiは、Aのi列をbに置き換えた行列をAiとして、
xi=det(Ai)/det(A)
と一意に解くことができ、クラメールの規則とかクラメルの公式などと呼ばれる。
A^-1を求めるとき、実用上は掃き出し法などの方が計算量の増加が穏やかだが、余因子展開の方が原理がわかりやすい。Aのi行めとj列めを除いた行列をAijと書き、余因子Δijを
Δij=(−1)^(i+j)*det(Aij)
と定義する。この余因子を要素とするi行j列の行列をA^(流儀によってはC)、それを転置したものをA~(余因子行列)として、ライプニッツの明示公式から行列式の多重線型性を確認すれば、
A^-1=(1/det(A))*A~
が成り立つことがわかる。
n個の関数(実関数でも複素関数でもよい)f1,f2...,fnが区間I上でn−1階微分可能とするとき、f1の0~n-1階微分を縦に並べた列ベクトルf1(x),f2の0~n-1階微分を縦に並べた列ベクトルf2(x)...,fnの0~n-1階微分を縦に並べた列ベクトルfn(x)を横に並べて作った行列(i行j列成分が、fjのi-1階微分になる)の行列式をロンスキー行列式W(f1,f2...,fn)という。ロンスキー行列式(ロンスキアン)が「恒等的に0」でないとき、f1,f2...,fnからなる関数族は線形独立な解をもつ。厳密な証明はさておき、拡大係数行列で連立方程式を解く操作を確認すれば、おそらくそうなのだという納得はできよう。関数族が線形従属である条件は難しいようで、ペアノなどが考察を与えているらしい。
-シリーズリンク-
次のメモ
 2021.06.28 09:39
|
2021.06.28 09:39
| 

